Picturing Quantum Software

Aleks Kissinger

Quantum Software Forum, TU Munich 2024


https://zxcalc.github.io/book

Quantum Software

the code that runs on a quantum computer

INIT 5
CNOT 1 0
H 2
Z 3
H 0
H 1
CNOT 4 2
...
 ↔

Quantum Software

code that makes that code (better)

Optimisation Simulation & Verification Error Correction

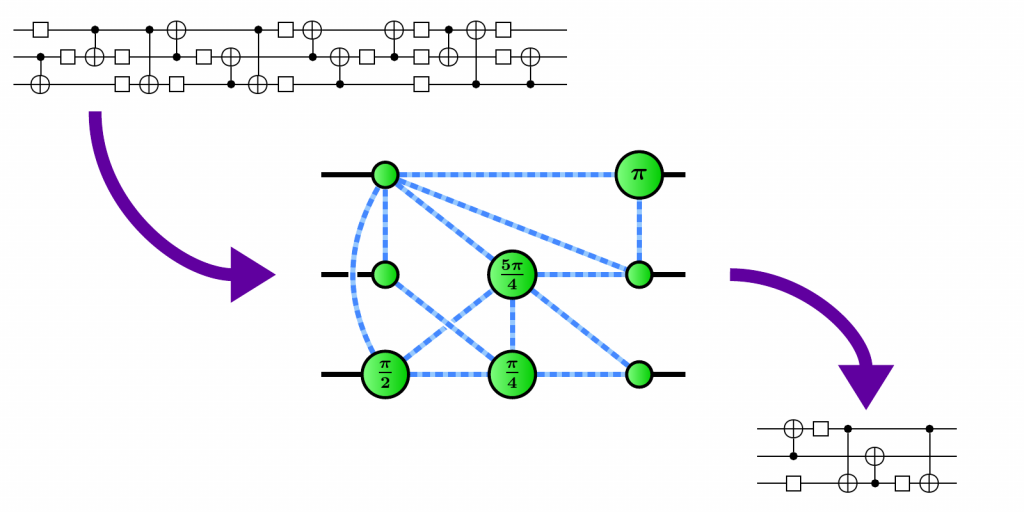
Optimising circuits the old-fashioned way

...

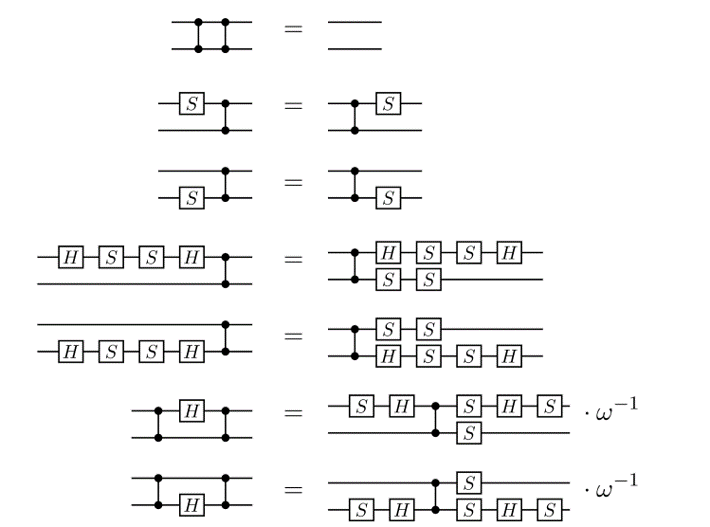
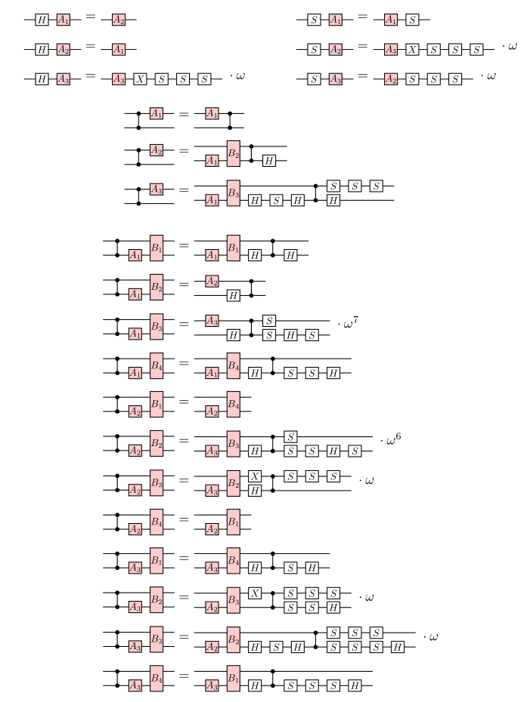
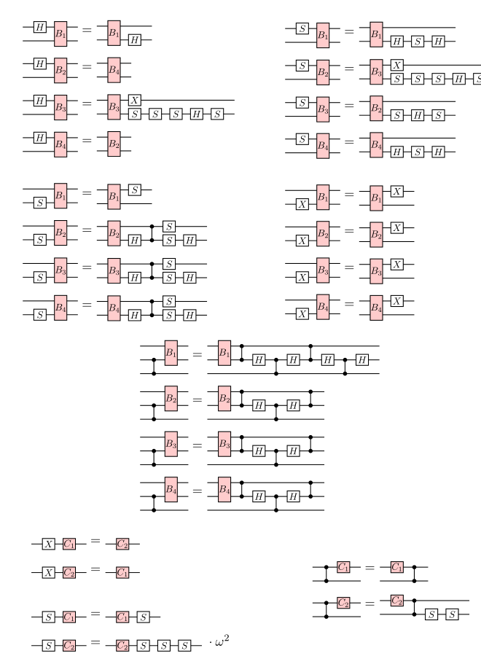
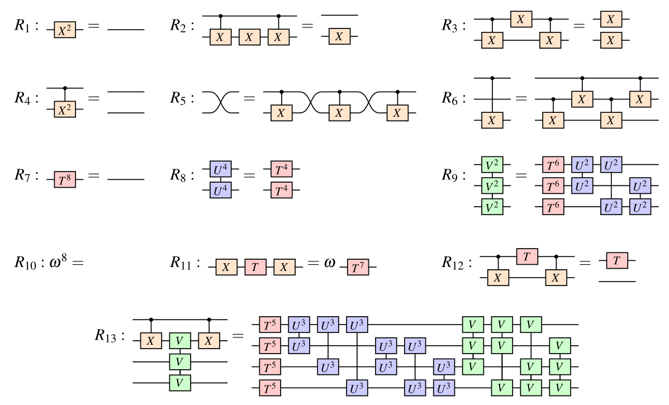
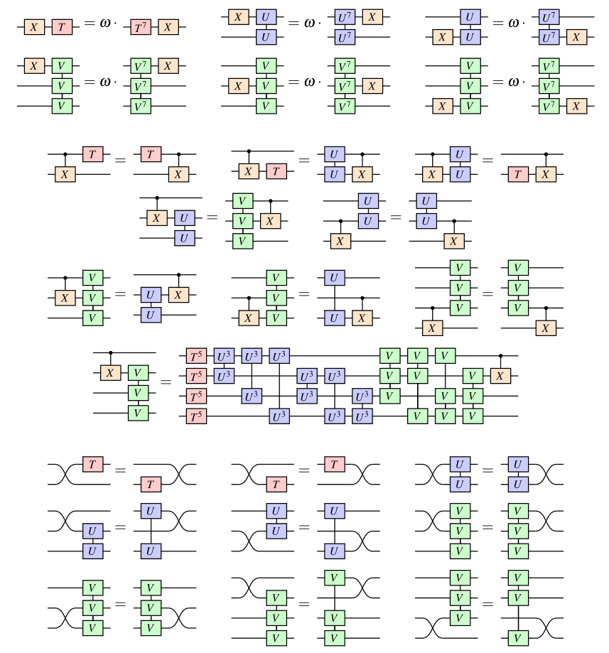
A better idea: the ZX calculus

A complete set of equations for qubit QC

Q: How to we scale up?

≈ 30 spiders

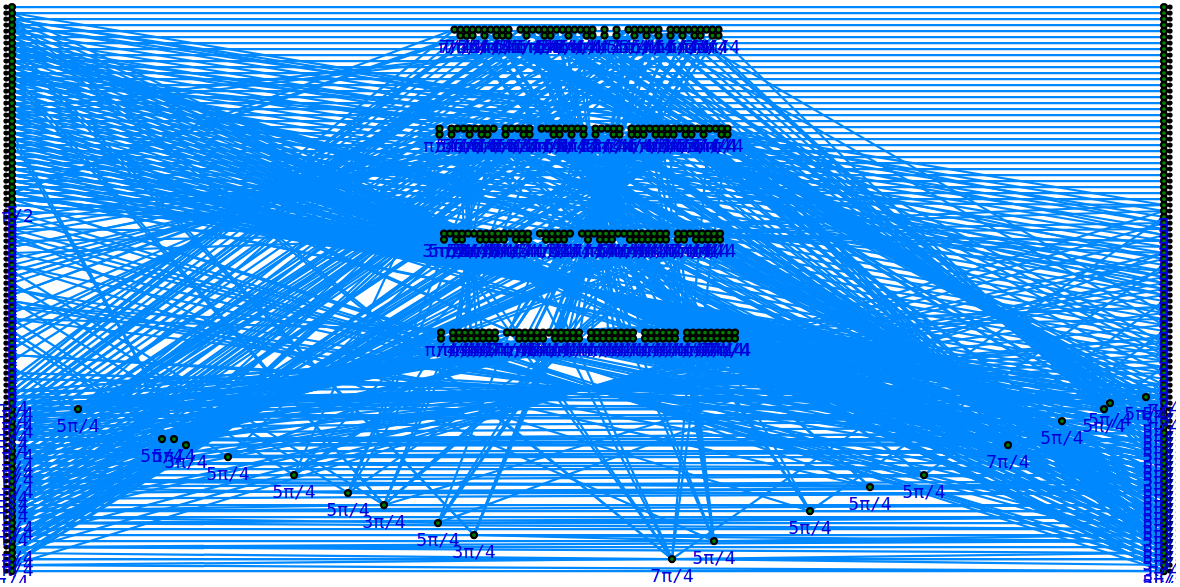≈ $10^3$ - $10^8$ spiders

A: Automation

PyZX

  • Open source Python library for circuit optimisation, experimentation, and education using ZX-calculus


https://github.com/zxcalc/pyzx

QuiZX


  • Large scale circuit optimisation and classical simulation library for ZX-calculus


https://github.com/zxcalc/quizx

ZXLive

  • GUI tool based on PyZX


https://github.com/zxcalc/zxlive

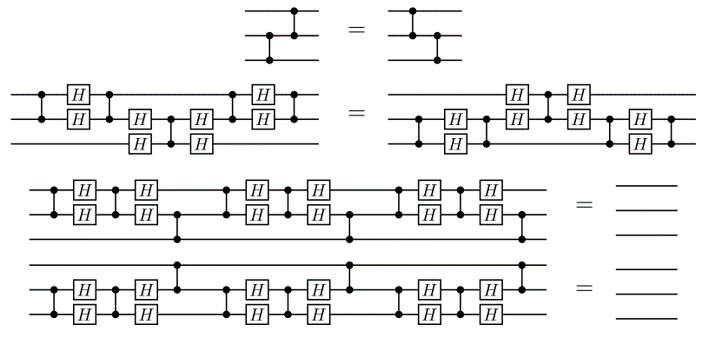
ZX Circuit Optimisation

...has 2 phases. First simplify...


$\Rightarrow$

ZX circuit optimisation

...and extract:

2-qubit gate count reduction



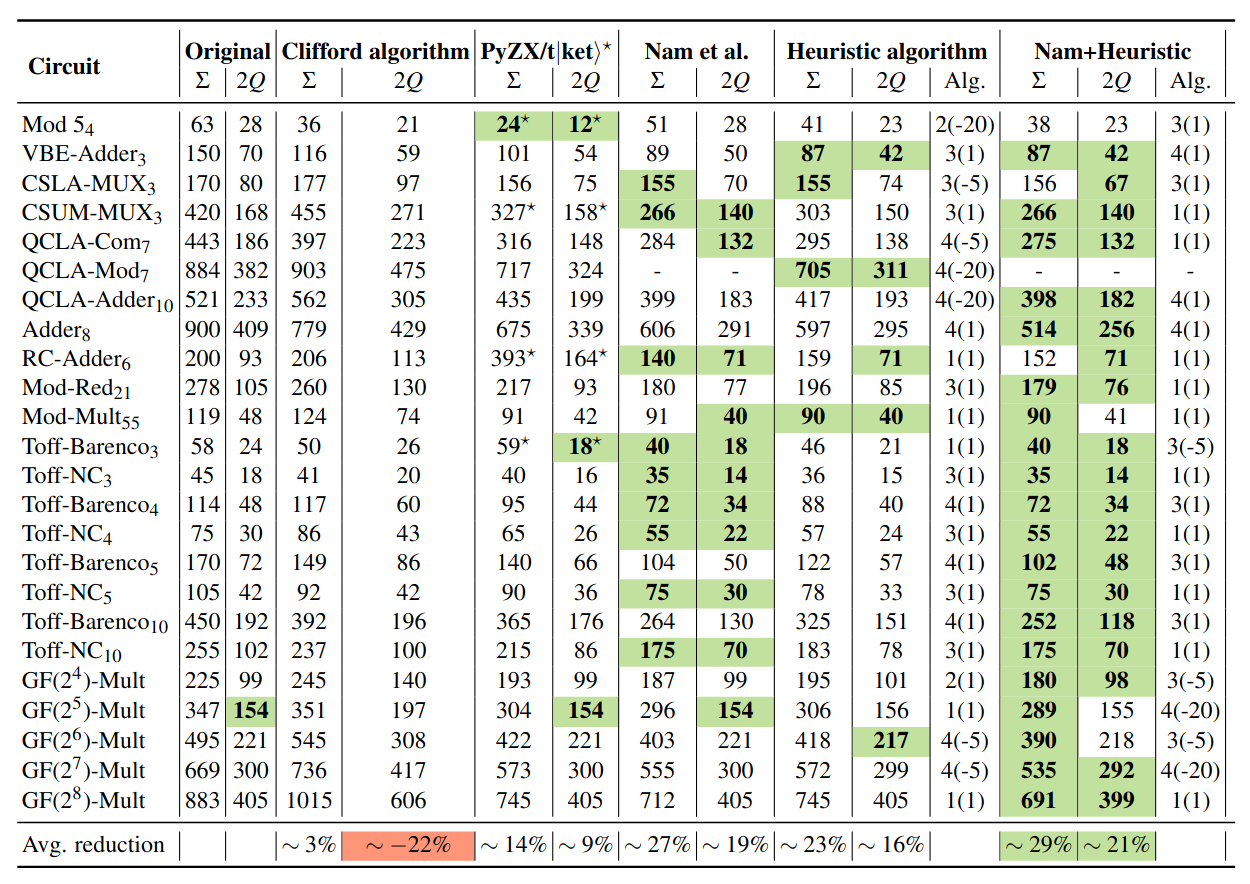
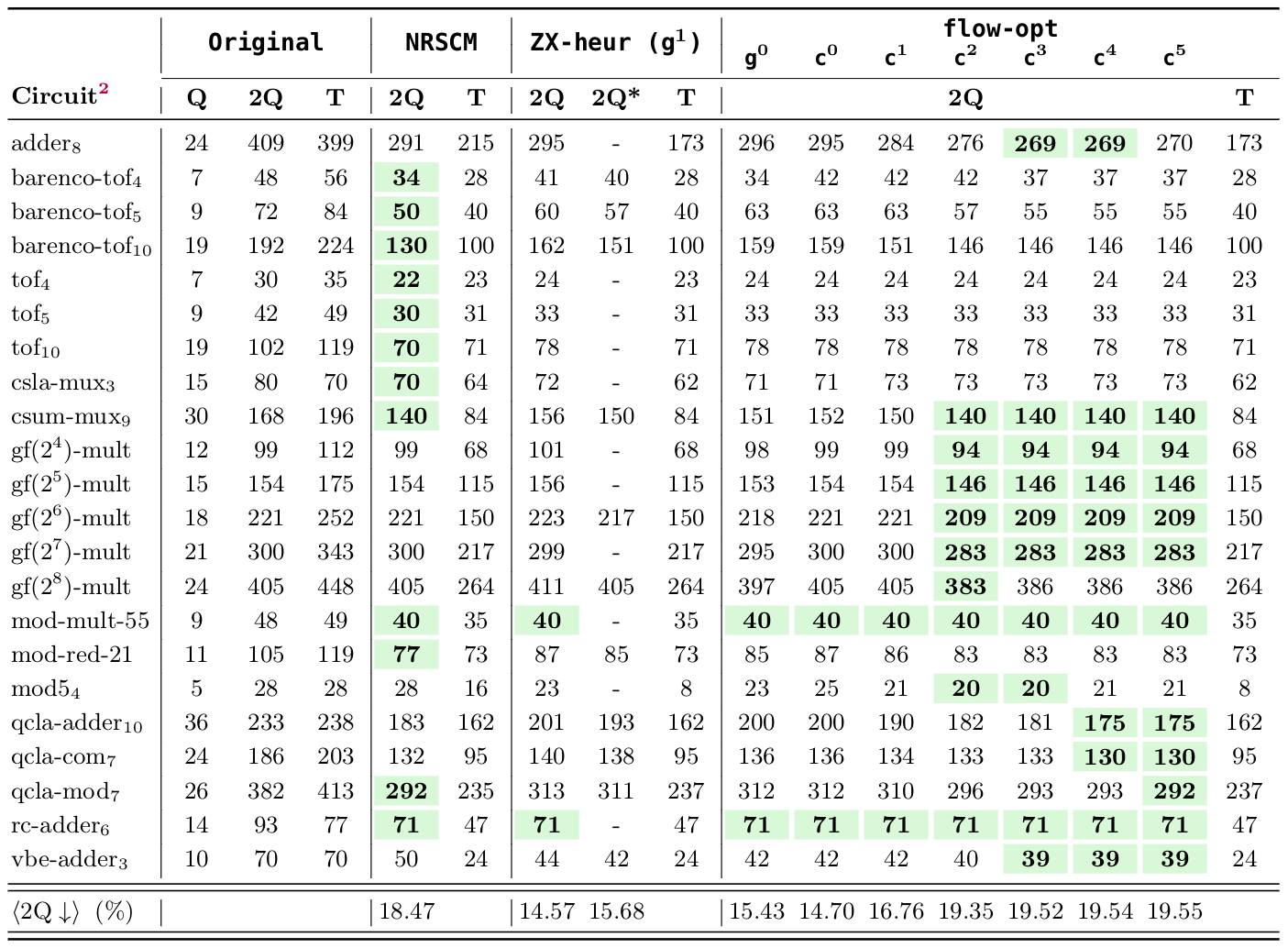
arXiv:2311.08881 | arXiv:2312.02793

T-count reduction



  • "Reducing the number of non-Clifford gates in quantum circuits". AK, van de Wetering. Phys Rev A 2020
  • "Optimal Compilation of Parametrised Circuits". van de Wetering, Yeung, AK. 2024 arXiv:2401.12877

Who cares about T-count anyway?

  • T-count is (probably) very important for fault-tolerant QC
  • Q: Why does it matter today?
  • A: Simulating quantum circuits on a classical (super)computer.

    →

Classical simulation

  • ...is hard (we think)
  • All known algorithms are exponentially hard in some measure of circuit size, e.g.

    # of qubits     tree width
                  T-count $\leftarrow$ stabilizer decompostion

  • Stabilizer rank decomposition: simulate a hard circuit by summing over LOTS of easy circuits

Stabilizer rank

The stabilizer rank of $|\psi\rangle$ is the least $N$ such that: \[ |\psi\rangle = \sum_{i=1}^N k_i |\xi_i\rangle \] for all $|\xi_i\rangle$ stabilizer states.


Gottesman-Knill $\implies$ amplitudes can be computed in $N \cdot$ poly time.

Stabilizer rank

  • Good stabilizer decompositions $\implies$ fast classical simulation
  • Hard to compute in general, but upper bounds exist:
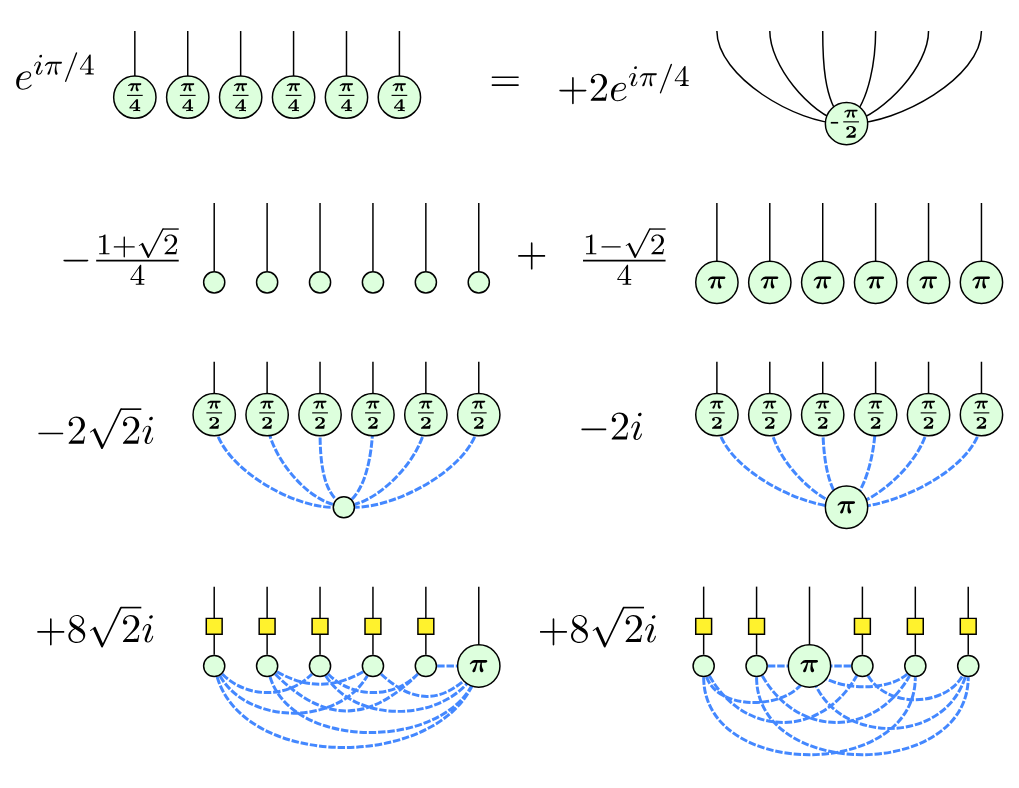
    • Naive: decomposing each T gate into 2 stabilizer terms, e.g.

      $T|{+}\rangle = |0\rangle + e^{i\pi/4} |1\rangle$

      gives $2^t$ terms.
    • Bravyi-Smith-Smolin decomposition of 6 T gates as 7 stabilizer terms:

      gives $2^{0.468t}$ terms.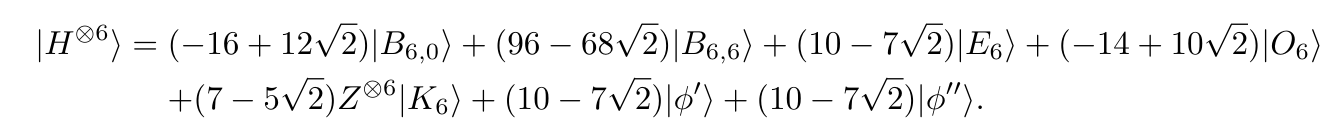

Idea: Do stabilizer decompositions on ZX diagrams!

Why?

  • Produces $7^{n/6} \approx 2^{0.468t}$ terms for $t$ T-gates
  • Interleaving ZX-simplification can make that significantly less

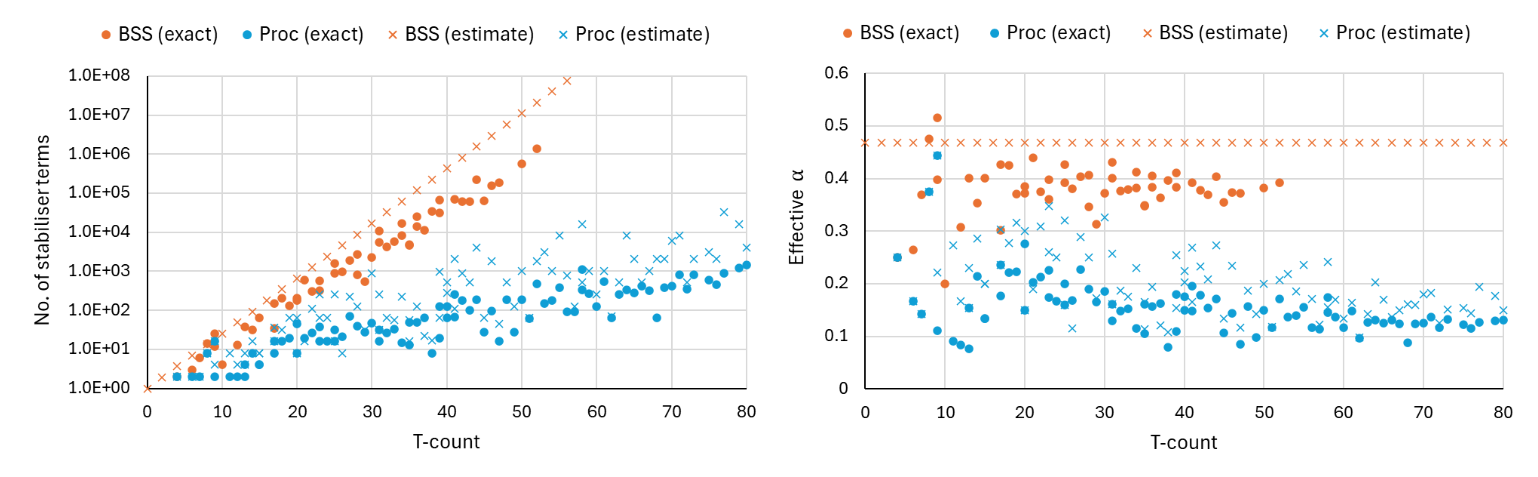
ZX-stabiliser decompositions

  • BSS decomposition: $2^{\alpha t}$ terms for $\alpha \approx 0.468$
  • SotA is $\alpha \approx 0.396$ (Qassim, Pashayan, Gosset 2021)
  • ZX-reduction $\Rightarrow$ much lower effective $\alpha$

    arXiv:2109.01076 | arXiv:2403.10964

Quantum error correction

...is done by encoding some space of logical qubits
into a bigger space of physical qubits:


  • $E$ (or just $\textrm{Im}(E)$) is a called a quantum error correcting code
  • QECCs are used to:
    • encode (and sometimes decode) logical states
    • measure physical qubits to detect/correct errors
    • do fault-tolerant computations on encoded qubits

Quantum error correction in ZX

two main approaches:

  • The graphical encoder approach

    $\quad \leadsto \quad$

  • The Pauli web approach

Graphical encoder

  • The idea: represent the encoder isometry $E$ directly as a ZX diagram

    $\quad = \quad$

  • Fault-tolerant QC $:=$ pushing through the encoder

Application: transversal Cliffords





» PQS, Chapter 11

Application: transversal non-Cliffords



...when $(L_X, S_X)$ is a triorthogonal code.

» PQS, Chapter 11

Application: lattice surgery



physical merge $\quad\qquad\leadsto\qquad\qquad\qquad\leadsto\qquad\quad$ logical merge


» PQS, Chapter 11

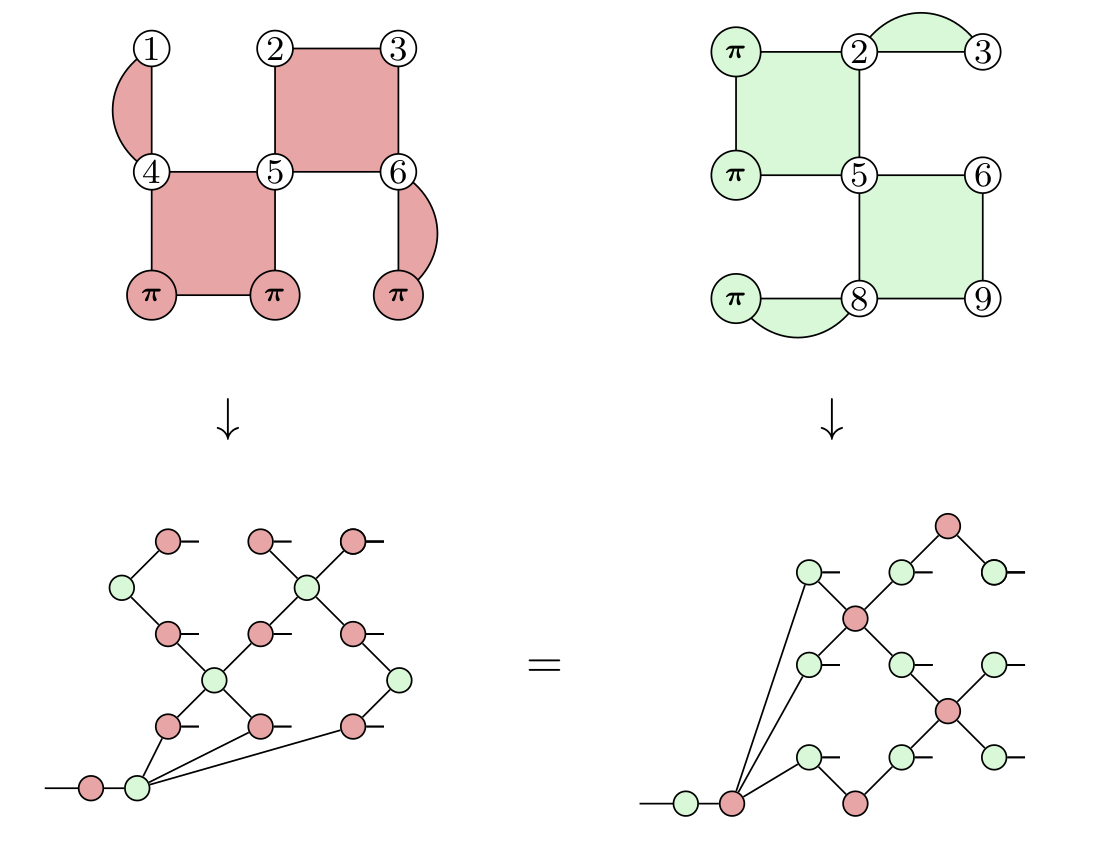
Application: CSS code transformations


arXiv:2307.02437

QEC in ZX

two main approaches:

  • The graphical encoder approach

    $\quad \leadsto \quad$

  • The Pauli web approach

Pauli webs

the motto: "circuits not codes"

  • Think of a (possibly infinite/periodic) sequence of gates and measurements as a "generalised" QECC

  • Physical qubits are the wires, logical qubits and QEC properties are defined by certain wire-colouring rules, called Pauli webs

Pauli webs

...can be used to study:

  • Stabiliser codes, using the circuit that measures all the stabilisers
  • Floquet codes, using a periodic sequence of (possibly non-commuting) Pauli measurements
  • More general "codes", where we just do stuff and see what the QEC properties are

Application: unifying FTQC



arXiv:2303.08829 (PsiQuantum)

Application: Floquetification

Distance-presv. transformations from stabiliser codes in Floquet codes

$\leadsto$
arXiv:2307.11136 | arXiv:2410.17240

https://zxcalc.github.io/book


https://zxcalculus.com
(>300 tagged ZX papers, online seminars, Discord)