Pseudospectra of Random Matrices:
The Non-Hermitian Anderson Model
The non-Hermitian Anderson model was first proposed by
Hatano and Nelson for the analysis of vortex pinning
in type-II superconductors [5].
This model has also been applied to the study of population dynamics [6].
The relevant "stochastic circulant" matrix is
 ,
where g is a constant and the diagonal entries are
drawn from some fixed probability distribution.
All unspecified entries are zero.
The circulant structure arises because the model describes
the motion of a particle along a ring.
The eigenvalues of this matrix
(for appropriate probability distributions)
form a "bubble with wings" in the complex plane.
Feinberg and Zee [2,3] and Goldsheid and Khoruzhenko [4]
have studied the location of the curves containing the
eigenvalues, and the eigenvalue density on that curve.
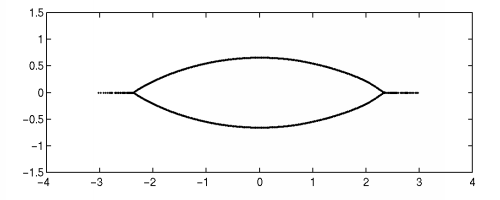
The eigenvalues for such an example are shown in Figure 1.
In the infinite dimensional case, the eigenvalues of the
corresponding Laurent operator have been studied by Davies [1].
|
Figure 1. Spectrum for one realization of the (circulant) non-Hermitian Anderson
model of dimension N=1000 with g=0.4.
The diagonal entries are uniformly distributed in [-1.5, 1.5].
|
The circulant non-Hermitian Anderson model typically exhibits
a mild degree of non-normality, as can be seen in Figures 2 and 3 below.
For small values of epsilon, the pseudospectra are located quite
close to the "bubble with wings"; in particular, note that the
pseudospectra have a hole in the middle.
|
Figure 2. Spectrum and epsilon-pseudospectra for a (circulant) non-Hermitian Anderson
model of dimension N=100 with g=0.4. The diagonal entries are uniformly distributed
in [-1.5, 1.5]. The values on the colorbar show log10(epsilon).
|
|
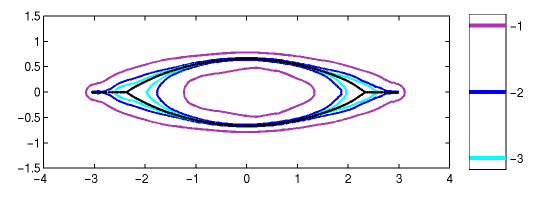
Figure 3. Spectrum and epsilon-pseudospectra for a (circulant) non-Hermitian Anderson
model of dimension N=1000 with g=0.4. The diagonal entries are uniformly distributed
in [-1.5, 1.5]. The values on the colorbar show log10(epsilon).
|
One can imagine instances where the ring structure that makes the above model
periodic is inappropriate.
If we remove the corner entries induced by that periodicity,
(and if the diagonal entries are real), then all the eigenvalues must be real.
Yet this matrix is highly non-normal and, for sufficiently large dimensions,
the borders of the pseudospectra capture the "bubble with wings" structure
observed for the matrix with corner entries.
Pseudospectra for two such matrices are shown in Figures 3 and 4 below.
|
Figure 4. Spectrum and epsilon-pseudospectra for a (non-circulant) non-Hermitian
Anderson model of dimension N=100 with g=0.4. The diagonal entries are uniformly
distributed in [-1.5, 1.5]. The values on the colorbar show log10(epsilon).
|
|
Figure 5. Spectrum and epsilon-pseudospectra for the (non-circulant) non-Hermitian
Anderson model of dimension N=1000 with g=0.4. The diagonal entries are uniformly
distributed in [-1.5, 1.5]. The values on the colorbar show log10(epsilon).
|
Bibliography
| [1] |
E. B. Davies,
Spectral properties of random non-self-adjoint matrices and operators,
Proc. Roy. Soc. Lond. Ser. A, to appear.
See math/0002159. |
| [2] |
J. Feinberg and A. Zee,
Non-Hermitean localization and de-localization,
Phys. Rev. E 59 (1999), 6433-6443.
See cond-mat/9706218. |
| [3] |
J. Feinberg and A. Zee,
Spectral curves of non-hermitian hamiltonians,
Nuc. Phys. B 522 (1999), 599-623.
See cond-mat/9710040. |
| [4] |
I. Ya. Goldsheid and B. A. Khoruzhenko,
Distribution of eigenvalues in non-Hermitian Anderson models,
Phys. Rev. Lett. 80 (1998), 2897-2900.
See cond-mat/9707230. |
| [5] |
N. Hatano and D. R. Nelson,
Localization transitions in non-Hermitian quantum mechanics,
Phys. Rev. Lett. 77 (1996), 570-573.
See cond-mat/9603165. |
| [6] |
D. R. Nelson and N. M. Shnerb,
Non-Hermitian localization and population biology,
Phys. Rev. E 58 (1998), 1383-1403.
See cond-mat/9708071. |
|
