Transients Menu

If a menu item in the table below is a hyperlink, click to see examples.

Matrix Powers	Create a new figure and plot \|\|A^k\|\| against k. A lower bound computed using the spectral radius will be shown as a black dashed line. Press the Stop button in that figure to terminate the computation. The lower bound (spectral radius)^k is drawn as a black dashed line.
Matrix Exponentials	Create a new figure and plot \|\|exp(tA)\|\| against t. A lower bound computed using the spectral abscissa will be shown as a black dashed line. Press the Stop button in that figure to terminate the computation. The lower bound exp(t*(spectral abscissa)) is drawn as a black dashed line.
Compute a Bound	Compute a lower bound based on the resolvent norm (pseudospectra) at a point you will be asked to select. This will be plotted as a green line on the Transient plot.
Best Estimate Lower Bound	Select the best lower bound based on all of the gridpoints used for the pseudospectra computation.
Information	Display a description of the lower bound computed using the above option.

Some specific examples

For these examples we use the Transient Demo, a matrix that is constructed to have transient behaviour in both its powers and exponentials. The eigenvalues and pseudospectra are shown below:

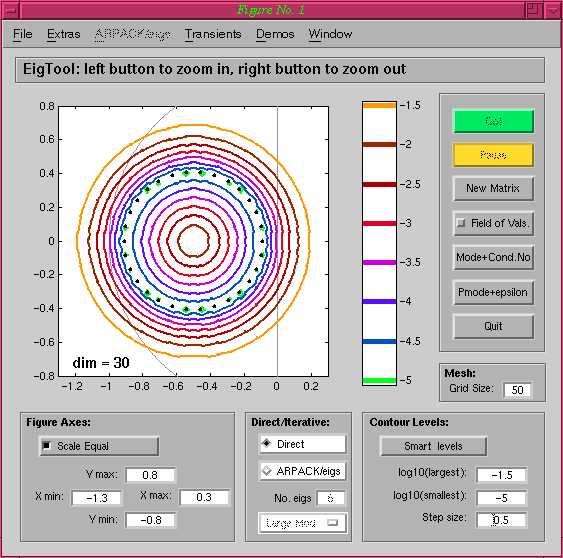
Note that the imaginary axis and unit circle are shown: these can be turned on using the menu options.

Matrix Powers

If we look at the norms of the powers of this matrix, we get the following plot after a few seconds of computation:

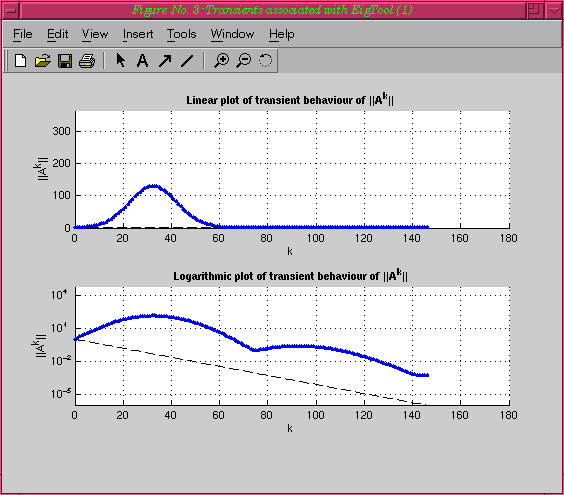
Although the largest eigenvalue (in absolute value) predicts the decay given by the black dashed line (it is inside the unit circle), the norm of the powers grows over one hundredfold before decaying as expected from the spectral radius [abscissa].

Matrix Exponentials

If we look at the norms of the matrix exponential exp(t*A) for various values of t, we get the following plot after a few seconds of computation. When prompted, we chose a time step dt=2:

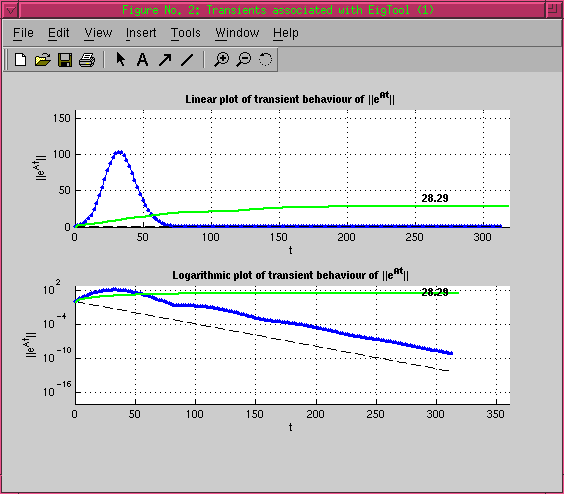
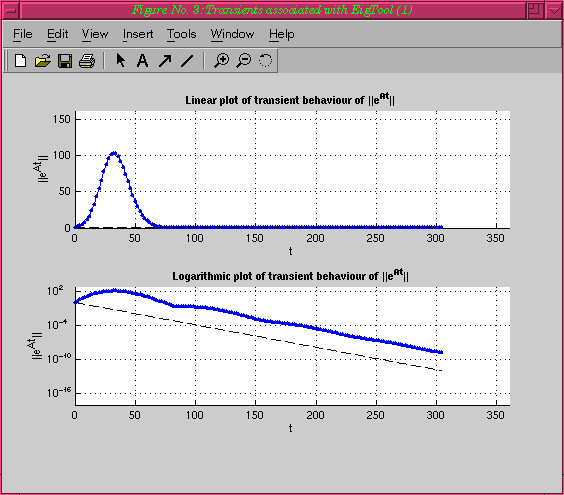
Transient behaviour of exponentials of A

Although the largest real part of an eigenvalue predicts the decay given by the black dashed line (it is in the left half-plane), the norm grows over one hundredfold before decaying according to the theory.

Compute a Bound

Using pseudospectra, it is possible to compute lower bounds on the size of this transient growth. After selecting this option, you will be asked to click on a point in the complex plane to base the bound upon; the bound is then computed as follows [1], where R is the resolvent norm at the selected point z. The bound will be computed over the values of k (or t) currently visable on the transient plot

For matrix powers:

max_{1<=k<=K}||A^k|| >= r^K/(1+(r^K-1)/((r-1)*(rR-1)))
(only valid for |z| = r > 1).

For matrix exponentials:

sup_{0<=t<=T}||exp(t*A)|| >=exp(a*T)/(1+(exp(a*T)-1)/(aR))
(only valid for Re(z) = a > 0).

Clicking on a point near z=0.2 gives the following plot:

Lower bound on the transient behaviour of exponentials of A

The bound appears as a green curve on the transient plot (with the selected point highlighted on the pseudospectra plot). For any particular point on this curve at step K (or time T), the bound says that the transient growth must have been at least this large for some point k < K (or t < T).

[1]: L. N. Trefethen, 2002, unpublished note

Best Estimate Lower Bound

As well as allowing the user to select a point to base their bound upon (see Compute a Bound), a best estimate of the lower bound over all of the points in the grid used for the current pseudospectra can be computed:

In general, this bound is usually within an order of magnitude of the true growth.

EigTool home page.