State of ZX 2024

Quantum Error Correction

Aleks Kissinger

ZX Seminar 2024

Quantum error correction

...is done by encoding some space of logical qubits
into a bigger space of physical qubits:


  • $E$ (or just $\textrm{Im}(E)$) is a called a quantum error correcting code
  • QECCs are used to:
    • encode (and sometimes decode) logical states
    • measure physical qubits to detect/correct errors
    • do fault-tolerant computations on encoded qubits

Quantum error correction in ZX

two main approaches:

  • The graphical encoder approach, adopted e.g. by the "grok" papers

    $\quad \leadsto \quad$

  • The Pauli web approach used e.g. by PsiQ and FU Berlin group

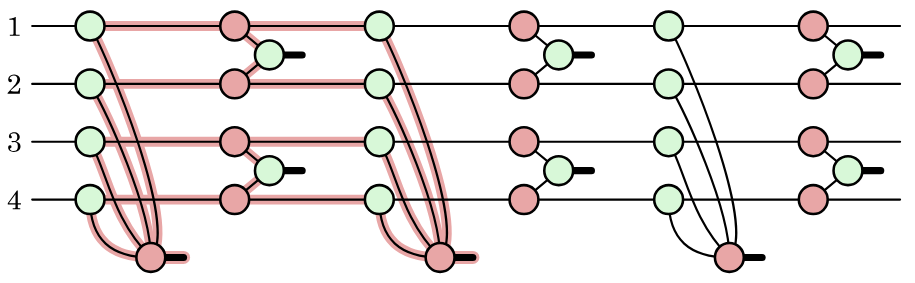
Graphical encoder

  • The idea: represent the encoder isometry $E$ directly as a ZX diagram

    $\quad = \quad$

  • ZX fragments $\leftrightarrow$ types of QEC codes
    • Clifford ZX-encoder $\leftrightarrow$ stabiliser codes
    • phase-free ZX-encoder $\leftrightarrow$ CSS codes
  • Fault-tolerant QC $:=$ pushing through the encoder

Stabiliser codes

  • QECCs whose subspace is fixed by a commutative subgroup $\mathcal S \subseteq \mathcal P_n$

    $\{ |\psi\rangle \, | \, \forall \vec P \in \mathcal S \ .\ \vec P|\psi\rangle = |\psi\rangle \} \cong \mathbb C^{2^k}$

  • $E$ is fixed by $m := n-k$ stabiliser generators:

    $\mathcal S = \langle \vec P_1 , \ldots, \vec P_m \rangle$      $(\vec P_j E = E)$

  • ...and $2k$ logical operators:

        

  • Detect/correct errors by measuring $\vec P_i$. The code distance $d$ is the weight of the smallest undetectable error $\leadsto [[n,k,d]]$

CSS codes

  • Calderbank-Shor-Steane codes are stabiliser codes whose generators split into "all-X" and "all-Z" parts:

    $\mathcal S = \langle \vec X_1 , \ldots, \vec X_{m_1}, \vec Z_1 , \ldots, \vec Z_{m_2} \rangle$

  • Equivalently, a pair of orthogonal subspaces $S_Z \perp S_X$ of $\mathbb F_2^n$ \[ \vec v \in S_X \qquad \leadsto \qquad X^{v_1} \otimes \ldots \otimes X^{v_n} \in \mathcal S \] \[ \vec v \in S_Z \qquad \leadsto \qquad Z^{v_1} \otimes \ldots \otimes Z^{v_n} \in \mathcal S \]
  • Generally easier than generic stabiliser codes, can import stuff from linear algebra and classical ECC or use...

Phase-free ZX diagrams

\[ :=\ \ |0...0\rangle\langle 0...0| + |1...1\rangle\langle 1...1| \]
\[ :=\ \ |{+}...{+}\rangle\langle {+}...{+}| + |{-}...{-}\rangle\langle {-}...{-}| \]
\[= \ \ N \sum_{\oplus_i b_i = 0} |b_1...b_n\rangle\langle b_{n+1}...b_{n+m}|\]

Normal forms

Phase-free ZX diagrams can be reduced efficiently to (pseudo-)normal form:



» PQS, Chapter 4

Special case: isometries

Isometry $\quad \implies \quad m \leq n ,\ \ j = 0$

\[ V :: |\vec x \rangle \mapsto \sum_{\vec y} |L \vec x + S \vec y\rangle \qquad L := \begin{pmatrix} 1 & 1 \\ 1 & 0 \\ 0 & 1 \\ 0 & 0 \end{pmatrix} \qquad S := \begin{pmatrix} 1 \\ 1 \\ 1 \\ 1 \end{pmatrix} \]
\[ X \text{ logical ops } := \{ X \otimes X \otimes I \otimes I, X \otimes I \otimes X \otimes I \} \] \[ X \text{ stabilisers } := \{ X \otimes X \otimes X \otimes X \} \]

\[ Z \text{ logical ops } := \{ I \otimes Z \otimes I \otimes Z, I \otimes I \otimes Z \otimes Z \} \] \[ Z \text{ stabilisers } := \{ Z \otimes Z \otimes Z \otimes Z \} \]

\[ V :: |\vec x \rangle \mapsto \sum_{\vec y} |L \vec x + S \vec y\rangle \]

Scalable notation:   » PQS, Chapter 10
Scalable CSS encoder:   » PQS, Chapter 11

Application: transversal Cliffords





» PQS, Chapter 11

Application: transversal non-Cliffords



...when $(L_X, S_X)$ is strongly triorthogonal.

» PQS, Chapter 11

Application: lattice surgery



physical merge $\quad\qquad\leadsto\qquad\qquad\qquad\leadsto\qquad\quad$ logical merge


» PQS, Chapter 11

Application: CSS code transformations


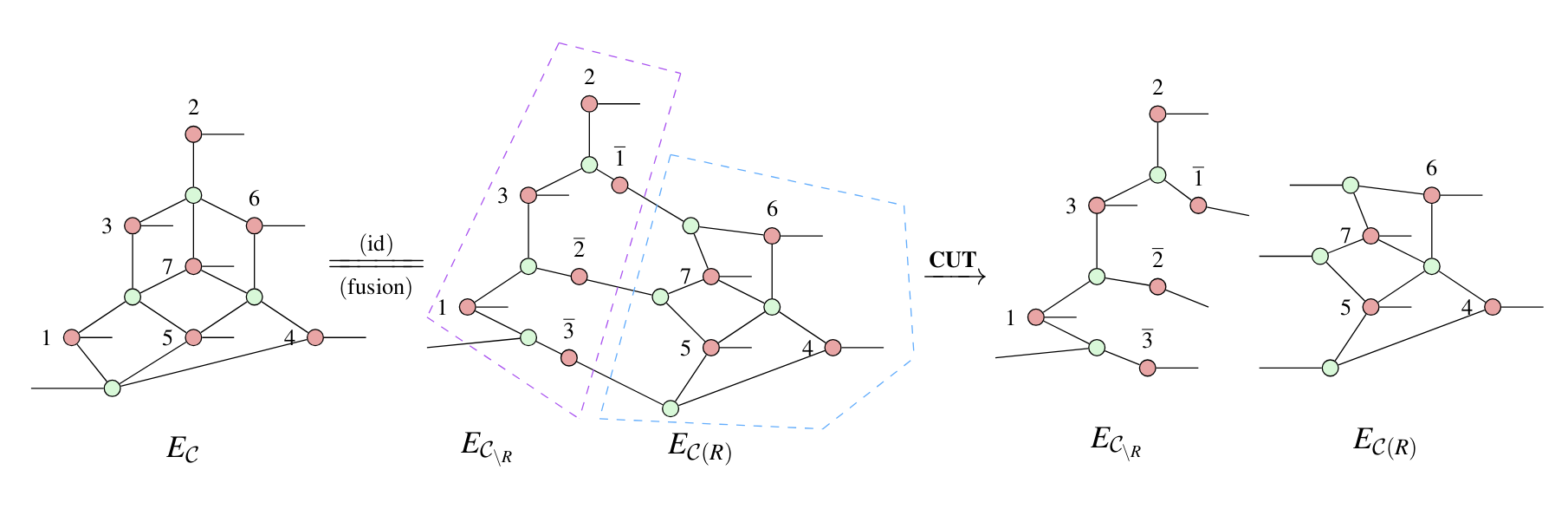
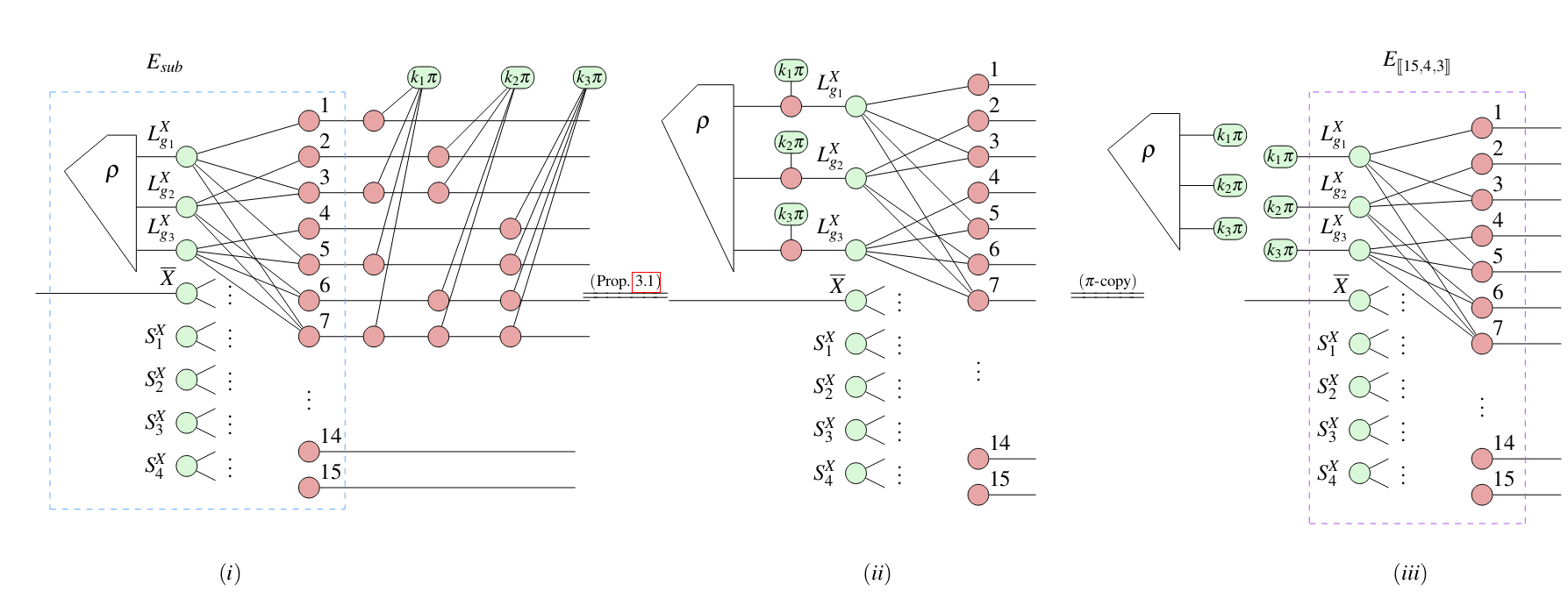
arXiv:2307.02437

Stabiliser encoders

  • Generic stabiliser codes $\implies$ $E$ is a Clifford ZX-diagram ($\alpha \in \{ j \cdot \frac\pi2 \}$)
  • Clifford ZX-diagrams have multiple efficiently-computable normal forms, e.g.
        
    GSLC form AP form

    » PQS, Chapter 5

Application: canonical forms for encoders

Variations on GSLC normal form give canonical forms for encoders, and allow convenient expressions of equiv. classes of codes.




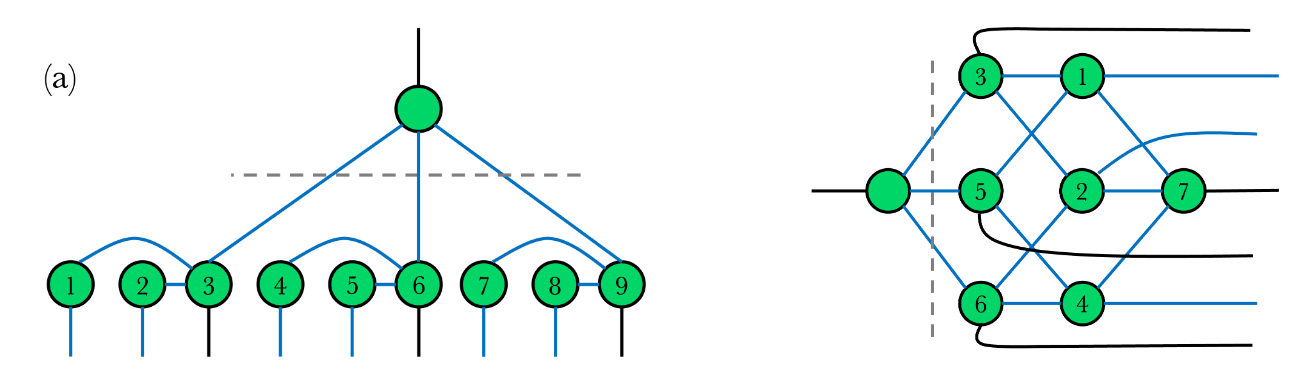
arXiv:2301.02356 | arXiv:2406.12083

Application: concatenated graph codes

Clifford ZX-calculus enables computing the
graph code of a concatenated graph code:



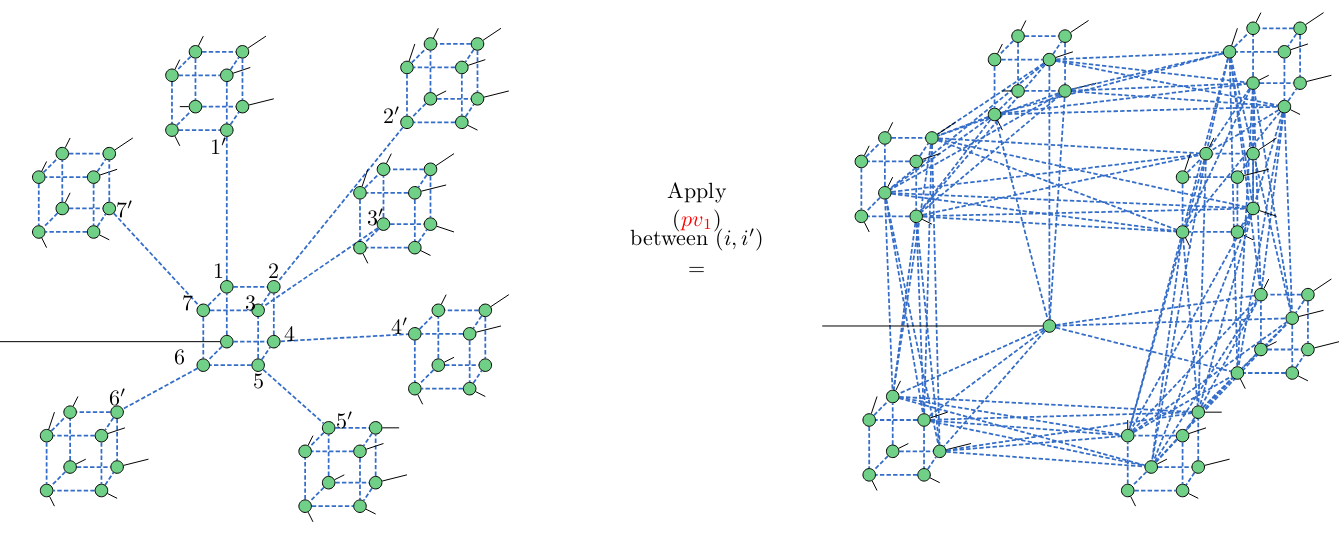
arXiv:2304.08363

QEC in ZX

two main approaches:

  • The graphical encoder approach, adopted e.g. by the "grok" papers

    $\quad \leadsto \quad$

  • The Pauli web approach used e.g. by PsiQ and FU Berlin group

Pauli webs

the motto: "circuits not codes"

  • Think of a (possibly infinite/periodic) sequence of gates and measurements as a "generalised" QECC

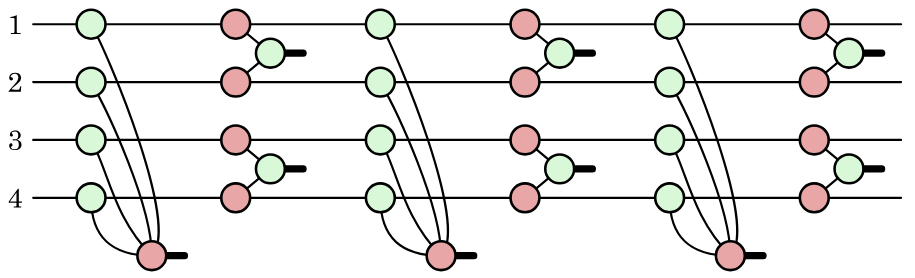
  • Physical qubits are the wires, logical qubits and QEC properties are defined by certain wire-colouring rules, called Pauli webs

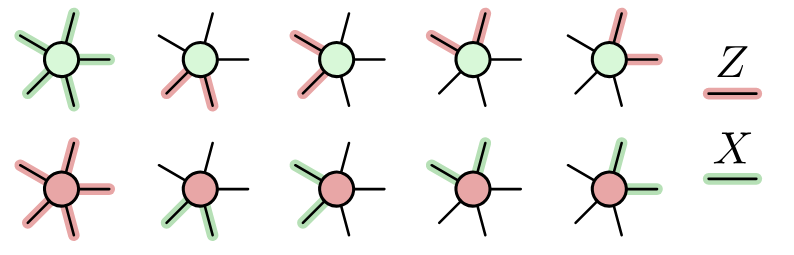
Pauli webs

...can be used to study:

  • Stabiliser codes, using the circuit that measures all the stabilisers
  • Floquet codes, using a periodic sequence of (possibly non-commuting) Pauli measurements
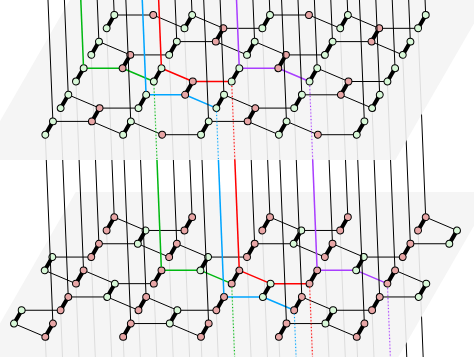
  • More general "codes", where we just do stuff and see what the QEC properties are

Application: unifying FTQC



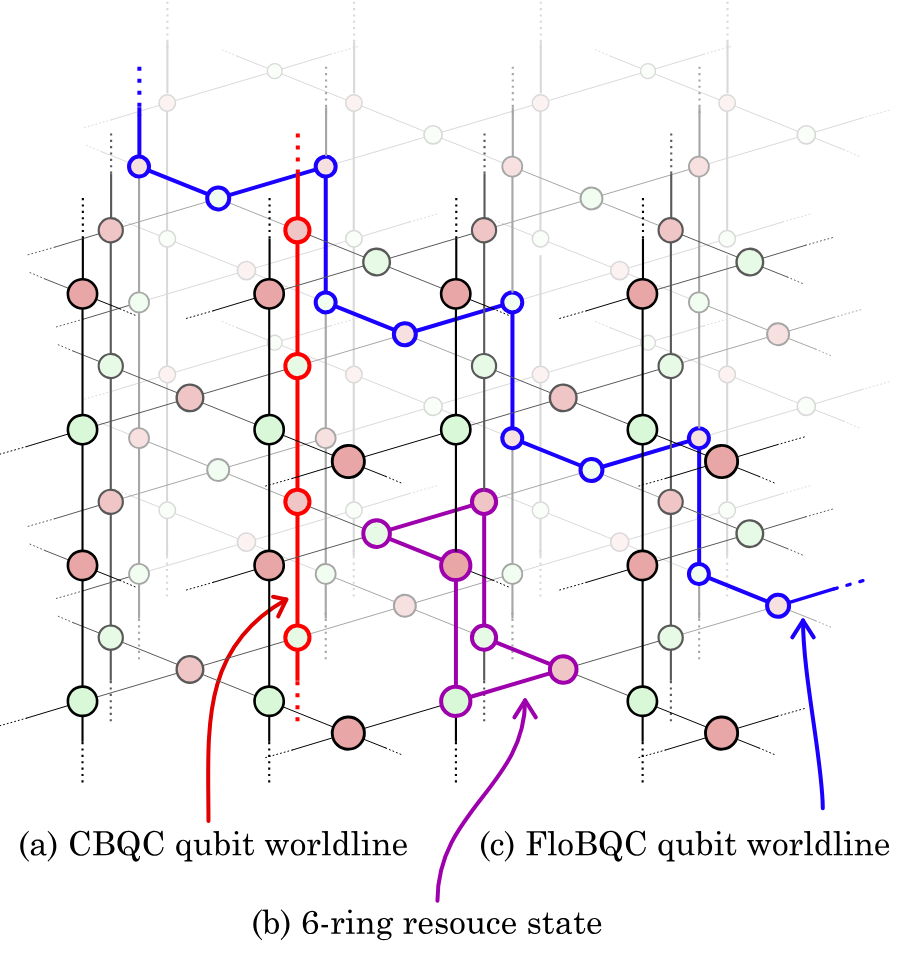
arXiv:2303.08829

Application: Floquetification

Distance-presv. transformations from stabiliser codes in Floquet codes

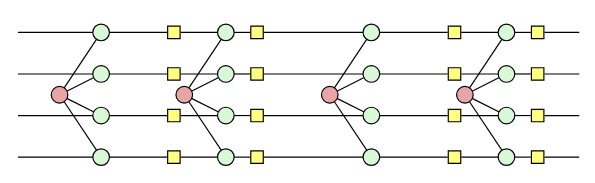$\leadsto$
arXiv:2307.11136

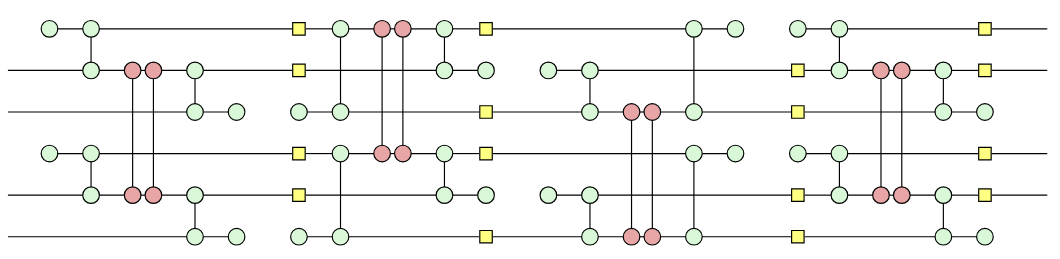
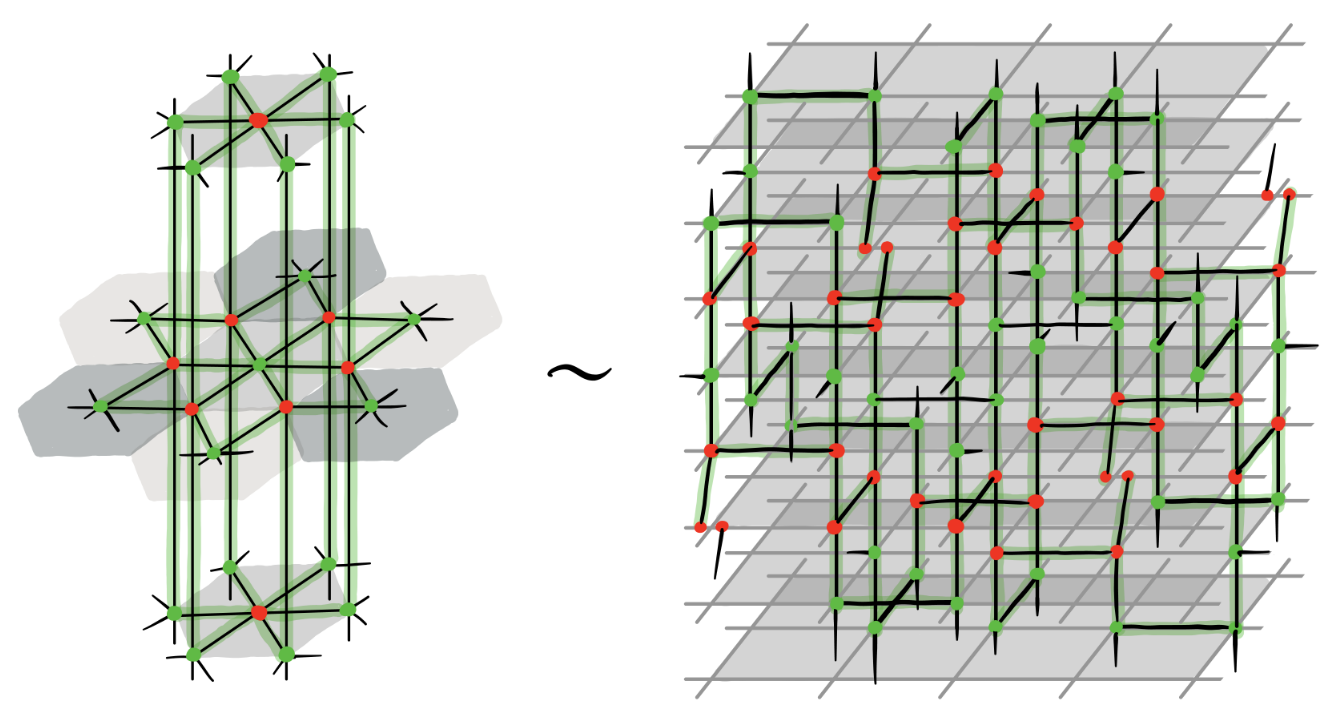
Beyond ZX-encoders and Pauli webs

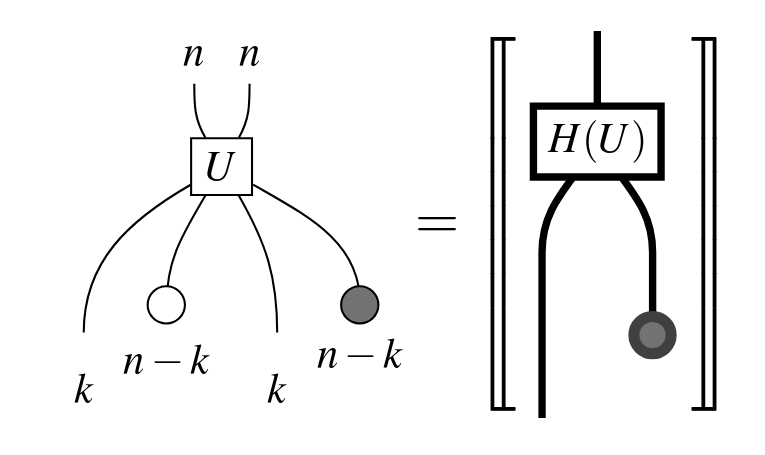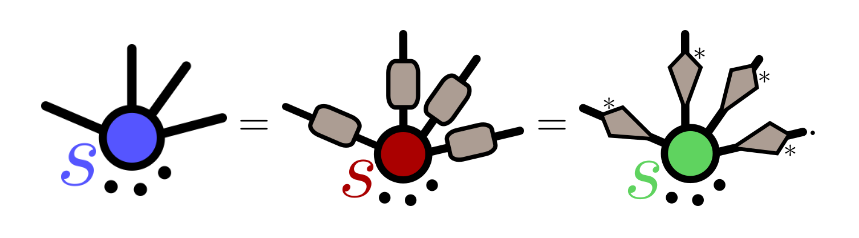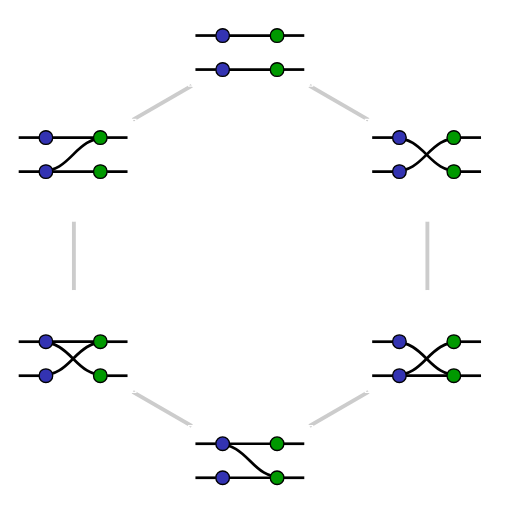Quopit stabiliser codes with graphical symplectic algebra XYZ ruby codes
with 3-color ZX variation		 Genon codes
arXiv:2304.10584 arXiv:2407.08566 arXiv:2406.09951


...and more: zxcalculus.com/publications.html