The spectral properties of dense nonsymmetric random matrices have been studied since the 1960s. Consider the n-dimensional matrix A whose entries are drawn from normal distribution with variance n^-1.

Figure 1. Dense random matrix with real entries, dimension N=10. The values on the colorbar show log10(epsilon).

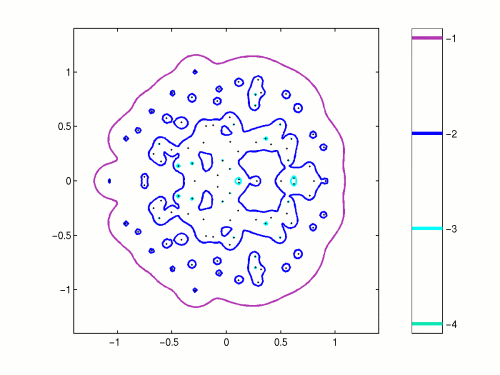
Figure 2. Dense random matrix with real entries, dimension N=100. The values on the colorbar show log10(epsilon).

Figure 3. Dense random matrix with real entries, dimension N=1000. The values on the colorbar show log10(epsilon).

Figure 4. Strictly lower triangular random matrix with real entries, dimension N=10. The values on the colorbar show log10(epsilon).

Figure 5. Strictly lower triangular random matrix with real entries, dimension N=100. The values on the colorbar show log10(epsilon).

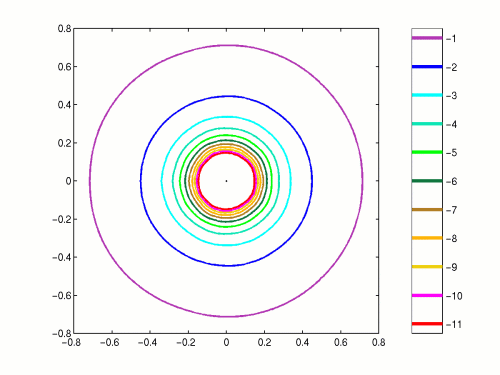
Figure 6. Strictly lower triangular random matrix with real entries, dimension N=1000. The values on the colorbar show log10(epsilon).

Figure 7. Strictly lower triangular random matrix with complex entries, dimension N=10. The values on the colorbar show log10(epsilon).

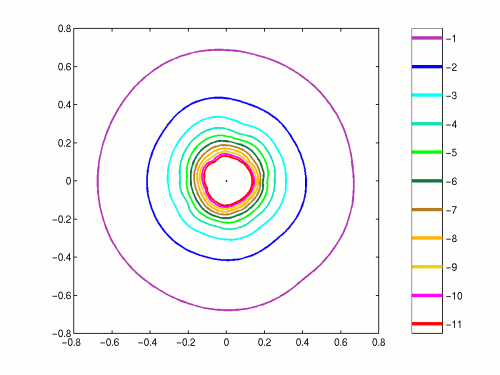
Figure 8. Strictly lower triangular random matrix with complex entries, dimension N=100. The values on the colorbar show log10(epsilon).

Figure 9. Strictly lower triangular random matrix with complex entries, dimension N=1000. The values on the colorbar show log10(epsilon).

Bibliography