Pseudospectra of a Toeplitz Matrix with a Piecewise Continuous Symbol
Dimension N=250

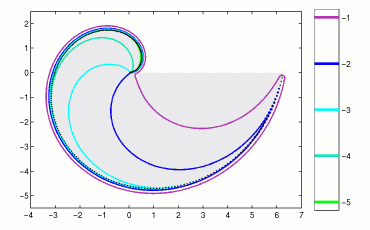
The colored lines denote the boundaries of pseudospectra of a Toeplitz matrix of dimension N=250 with a piecewise continuous symbol. The gray region shows the spectrum of the infinite dimensional Toeplitz operator on l₂(N). For N sufficiently large, each of the illustrated pseudospectra will include the spectrum of the infinite dimensional operator, but for this class of piecewise continuous symbols, this value of N needs to be especially large. The eigenvalues of this example have been studied by Basor and Morrison ("The Fisher-Hartwig conjecture and Toeplitz eigenvalues", Linear Algebra Appl. 202 (1994), 129-142); pseudospectra are illustrated in [BET00].

Further details about this example can be found on the page:
Pseudospectra of Toeplitz Matrices and Operators: Matrices with Piecewise Continuous Symbols.

Use the following MATLAB code compute pseudospectra for this example using EigTool. Note that the above plot would use N=250 below.

    N = 50;
    r = -i./[1:N]; c = [-i pi i./[1:N-2]];
    T = toeplitz(c,r);
    opts.npts = 50;
    opts.ax = [-4 7 -6 3];
    opts.levels = [-5:-1];
    eigtool(T, opts)